Reports on Mandelbrot Activities
Contents
Reports on Mandelbrot Activities#
Mandelbrot Activity 1#
Read the Wikipedia entry on the Mandelbrot set, and the entry on Mandelbrot. Mandelbrot’s educational books and papers are amazing, and amazingly clearly written. If you don’t come back from this activity, well, at least you left going in a good direction.
Our thoughts: Welcome back! One of the things we find most inspiring about Mandelbrot was his observation of how close many open, deep mathematical problems were to the simplest material taught in ordinary mathematics classes. We hope to demonstrate that principle with this OER, of course, but we can only hope to approach his clarity, on our best days.
Mandelbrot Activity 2#
Prove by induction that the degree of the \(n\)th Mandelbrot polynomial \(p_k(c)\) is \(2^{n-1}\) for \(n\ge 2\), and that the leading coefficient is \(1\).
The base of the induction is that \(p_2(c) = c^2+c\) which has degree \(2^{2-1} = 2\) and leading coefficient \(1\). If we then suppose that the degree of \(p_k(c)\) is \(2^{k-1}\) and its leading coefficient is \(1\), then since \(p_{k+1} = p_k^2 + c\) we have deg \(p_k = 2\cdot2^{k-1} = 2^k\) and the leading term is \(c\) to this power so the leading coefficient is \(1\).
Mandelbrot Activity 3#
Prove that \(c=-2\) and \(c=0\) are both in the Mandelbrot set. Show that all zeros of Mandelbrot polynomials give periodic orbits under the Mandelbrot iteration and are thus in the Mandelbrot set.
a) If \(c=0\) then all \(z_k = 0\) thereafter, which is bounded; so \(c=0\) is in the Mandelbrot set. b) If \(c=-2\) then \(z_0 = 0\), \(z_1 = -2\), \(z_2 = -2 + 4 = 2\), \(z_3 = 4 -2 = 2\), and indeed \(z_k = 2\) for all \(k\ge 2\). So \(c=-2\) is in the Mandelbrot set. c) If \(z_k(\xi) = 0\), then \(z_{k+1}(\xi) = z_k^2(\xi) + \xi = \xi\) and this is also \(z_1(\xi)\); we are clearly repeating. Counting Python-style from zero, the entities \(z_0\), \(z_1\), \(\ldots\), \(z_{k-1}\) might have been different but \(z_k = z_0\) so the cycle has period \(k\). Notice that if \(m | k\) (that is, \(m\) divides \(k\)) it might be true that \(z_m(\xi) = 0\) as well, in which case this point has a lower period as well. Notice that all points of period \(2\) are also of period \(4\), period \(6\), and so on; but that there are points of period \(4\) which are not points of period \(2\). This means we can factor Mandelbrot polynomials of composite order, that is, if their \(k\) is a composite integer.
Mandelbrot Activity 4#
Is \(i = \sqrt{-1}\) in the Mandelbrot set?
\(z_0 = 0\), \(z_1 = i\), \(z_2 = i + i^2 = i -1\), \(z_3 = (i-1)^2 + i = -1 -2i + 1 + i = -i \), \(z_4 = -1 + i\), \(z_5 = 1 -2i +i^2 + i = -i\) and we are repeating, so yes, \(i\) is in the Mandelbrot set.
Mandelbrot Activity 5#
Prove that the Mandelbrot polynomials are unimodal. At the time we write this, this question is open: solve it, and you could publish a paper with your proof (Maple Transactions would be a good place). The word “unimodal” just means that the size of the coefficients increases to a peak, and then decays again. As in \(z_4\), the peak might be attained by two coefficients, not just one. Seriously, we don’t know how to prove this. We think it’s true, though.
Seriously, we couldn’t do this one. Your Answer Goes Here. We’d really like to see it.
Mandelbrot Activity 6#
Solve \(z_3 = 0\) by hand, as follows. First, divide out the visible root, \(c=0\), to get the cubic equation \(0 = 1 + c + 2c^2 + c^3\). Then put \(c = \xi - 2/3\) so \(c^3 = (\xi -2/3)^3 = \xi^3 - 2\xi^2 + 4\xi/9 - 8/27\) which will transform the equation into a cubic in \(\xi\) of the form \(0 = q + p\xi + \xi^3\). Then put \(\xi = u + v\) (introducing two new variables seems like the opposite of progress, but trust us, it will help). This transforms the equation to \((u+v)^3 + p(u+v) + q = 0\), or \(u^3 + 3uv(u+v) + p(u+v) + q = 0\). Show that if you can find \(u\) and \(v\) that simultaneously solve \(3uv + p = 0\) and \(u^3 + v^3 + q = 0\) then you can solve the original equation. Do so. Your formula at the end should give you three, and only three, roots. Write out your answer explicitly, and compare it with (say) the answer from Wolfram Alpha. There is an analogous formula for quartics, but even teaching this cubic formula is considered cruel and inhumane; well, it would be if you were to be tested on it. But maybe a public competition for solving cubics might be entertaining for the spectators, as it seems to have been in 1530. Quite amazingly, at least to him, RMC had recent recourse to this method in order to write a very fast program to evaluate the cube roots of an equation that depended on a parameter, except that the equation was of the form \(x^3 + mx^2 + n=0\) (which was apparently the type that defeated Fior in the contest—but just solve for \(1/x\) instead, and that puts it into the previous form). All modern computer algebra systems know how to solve cubics and quartics in terms of radicals; quintics cannot, in general, be solved in terms of radicals, but they can be solved in terms of elliptic functions. Now there’s a rabbit hole for you.
We really did this one, but there’s not much reason to type it out. You can check your own answers by evaluating all three of them in floating-point and running the Mandelbrot iteration on them. All three should have \(z_3(c)\) approximately zero.

Fig. 17 The page on the left had a sign error. Rather than track it down, it was easier to start again.#

Fig. 18 The real solution was verified numerically to 10 decimal places on the calculator. The other two roots can be found by computing the other cube roots for u.#
Mandelbrot Activity 7#
Prove by induction that the code MandelbrotWithDerivative computes the correct derivative of every Mandelbrot polynomial. Rather, that it would compute the correct derivative if the underlying arithmetic were exact. You might need what is known as a loop invariant: something that is true before the loop starts, and is true at the start of every iteration, and at the end of every iteration (though not necessarily true after each intermediate step of the iteration). But this loop is simple enough that a direct induction also works.
def MandelbrotWithDerivative(n: int, c):
dz = 0*c
z = 0*c # try to inherit the type of c
for i in range(n):
dz = 2*z*dz + 1 # A bit iffy to add constants to Polynomials in Python, but maybe it works. Yes! It does!
z = z*z + c
return(z,dz)
Before the loop begins, both \(z = z_0 = 0\) and \(dz = z_0'(c) = 0\).
A loop invariant just after the : is that z \(= z_{i-1}(c)\) and dz \(= z_{i-1}'(c)\).
After the statement
dz = 2*z*dz + 1
we have dz = \(z_{i}'(c) = 2z_{i-1}(c)\cdot z_{i-1}'(c)+1\) because \(d/dc\) applied to \(z_i = z_{i-1}^2 + c\) gives exactly that.
After the statement
z = z*z + c
we have z \( = z_i(c)\) by definition. So at the end of the loop, we have z \(= z_{i}(c)\) and dz \(= z_{i}'(c)\). Incrementing \(i\) and going to the top of the loop we satisfy the loop invariant.
The loop terminates if i==n at the top, and the code returns \(z_i(c)\) and \(z_i'(c)\) where \(i=n\).
Mandelbrot Activity 8#
Are the zeros of the derivatives of the Mandelbrot polynomials in the Mandelbrot set? We think so, but we haven’t written out the proof.
We should check at least one example. \(z_3(c) = c^3 + 2c^2 + c + 1\) so \(z_3'(c) = 3c^2 + 4c + 1\) which has zeros given by the quadratic formula:
so we can try these numbers out in the Mandelbrot iteration. Sure enough, the iteration remains bounded.
We seem to remember a kind of “mean value theorem” for complex numbers that says that zeros of the derivative can be found in the convex hull of the zeros. We also seem to remember that the Mandelbrot set is connected. Something might be do-able along these lines. As we said, we have not proved this (and it might not be true).
Mandelbrot Activity 9#
“A good numerical method gives you the exact solution to a nearby problem”. This is an informal definition of numerical stability. An algorithm is “numerically stable” if it gives you the exact solution, not to the problem you were trying to solve (say the polynomial \(z(c) = 0\)) but instead to a nearby problem, say \(z(c) - 10^{-16}i = 0\). Some problems, however, are sensitive to changes (in the vernacular of numerical analysis, ill-conditioned). Consider the polynomial \(z(c) = \sum_{k=0}^d a_k c^k\) and a perturbed (changed) polynomial \(z(c) + \Delta(c) = \sum_{k=0}^d a_k(1+s_k) c^k\) where the coefficients \(a_k\) have all been changed by small relative amounts \(s_k\). Suppose further that all \(|s_k| \le t\), some tiny number. By using the triangle inequality, show that \( | \Delta(c) | \le K(c) t \) where \( K(c) = \sum_{k=0}^d |a_k| |c|^k \) This number \(K(c)\) serves as a kind of condition number for the polynomial: the larger it is, the more sensitive the polynomial is. Plot the condition numbers (on a log scale!) of the Mandelbrot polynomials \(z_6(c)\) and \(z_7(c)\) on \(-2 \le c \le 0\).
The proof runs along the lines suggested in the activity and can be seen at this video. For the graph, see Figure 2 in Some Facts and Conjectures on Mandelbrot Polynomials
Mandelbrot Activity 10#
Pseudozeros. The zeros of \(z(c) - 10^{-k}\exp(i\theta)\) for \(k=6\), say, represent a curve in \(c\) space (let \(\theta\) vary from \(-\pi\) to \(\pi\) so the tiny perturbation \(10^{-6}\exp(i\theta)\) turns a full circle in the complex plane). As \(k\) is taken larger, one expects these curves to surround the zeros of \(z(c)\) itself. Graph some pseudozeros of a Mandelbrot polynomial.
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
from numpy import linalg as LA
import cmath
import time
import scipy.linalg
def p_mand(z, n):
p = 0
for i in range(n):
p = z*p*p + 1
return(p)
# Activity 10: Pseudozeros (with explicit perturbation and contours)
n = 5
N = 250
e = 0.001
z = sym.Symbol('z')
p5 = p_mand(z, n)
p5_coeffs = sym.Poly(p5, z).coeffs()
fig = plt.figure(figsize=(10, 8), dpi = 80)
plt.xlabel('Re(z)')
plt.ylabel('Im(z)')
for i in range(N):
perturb_vector = (1 + np.random.rand(1, 2**(n-1))*e).tolist()[0]
perturb_coeffs = [a*b for a,b in zip(p5_coeffs, perturb_vector)]
pn_soln_perturbed = np.roots(perturb_coeffs)
X = [np.real(x) for x in pn_soln_perturbed]
Y = [np.imag(x) for x in pn_soln_perturbed]
plt.scatter(X, Y, s = 1, c = 'black')
nx, ny = (1500, 1500)
x = np.linspace(-2.5, .5, nx)
y = np.linspace(-1.25, 1.25, ny)
[X, Y] = np.meshgrid(x, y, indexing='ij')
Z = np.zeros((nx, ny))
for i in range(nx):
for j in range(ny):
Z[i, j] = abs(p_mand(complex(X[i, j], Y[i, j]), n))/p_mand(abs(complex(X[i, j], Y[i, j])), n)
plt.contour(X, Y, Z, [e])
plt.show()
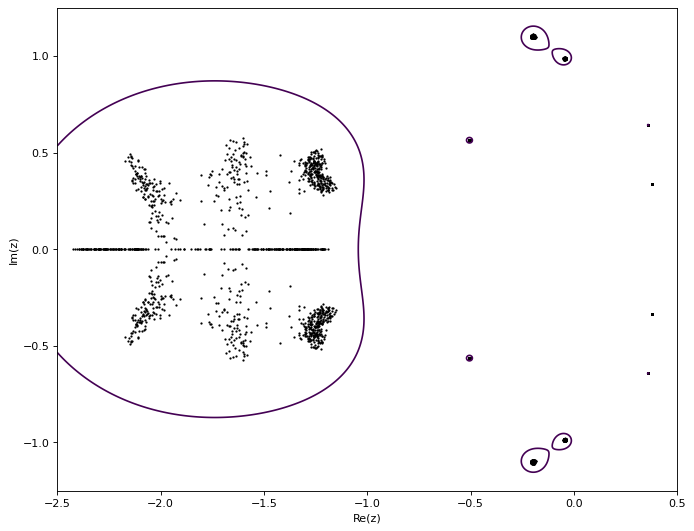
Mandelbrot Activity 11#
Write \(\mathbf{C} = \mathbf{A}\mathbf{B}^{-1}\) and show that the generalized eigenvalues of \(\mathbf{A}-\lambda\mathbf{B}\) are the simple eigenvalues of \(\mathbf{C} - \lambda\mathbf{I}\). Find \(\mathbf{C}\) for the Mandelbrot matrices above, and code it up and compare the times to compute simple eigenvalues versus generalized eigenvalues. How high a degree can you get to? We stopped at \(N=16\), where the computation took about an hour and a half, and the residual was about \(4.0e-5\). The current record is held by MPSolve with \(k=23\), so over \(4\) million roots (using multiple precision); we don’t think eigenvalue methods can get that high, but we think homotopy methods can, although they haven’t yet.
We gave part of what to do, already in the question. Here’s some code.
# This matrix gives a _simple_ eigenvalue problem for Mandelbrot polynomials: see Activity 10 above.
def m_mand(n):
M = np.array([-1])
for i in range(2, n):
temp = M
d = 2**(i) - 1
M = np.zeros((d, d))
d = 2**(i-1) - 1
M[0:d, 0:d] = temp
M[d+1:, d+1:] = temp
M[d, d-1] = -1
M[d+1, d] = -1
M[0, -1] = -1
return(M)
N = 12
times = []
for i in range(3, N+1):
M = m_mand(i)
tic = time.perf_counter()
LA.eig(M)
toc = time.perf_counter()
times.append(toc - tic)
# Should also plot line of best fit and find slope
plt.scatter(np.power(2, list(range(2, N))) - 1, times)
plt.yscale('log')
plt.xscale('log')
plt.show()
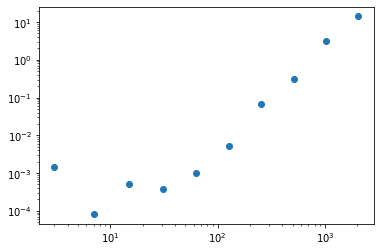
Mandelbrot Activity 12#
Eigenvalues of perturbed matrices are called pseudospectra (the set of eigenvalues themselves is called the spectrum). \(\Lambda_\varepsilon(\mathbf{A}) := \{z : \exists \mathbf{E} \backepsilon \mathrm{det}(z\mathbf{I} - (\mathbf{A}+\mathbf{E})) = 0 \& \|\mathbf{E}\| \le \varepsilon\}\). That definition means, in words, that the pseudospectrum at size \(\varepsilon\) is the set of complex numbers \(z\) that are the exact eigenvalues of matrices perturbed by another matrix \(\mathbf{E}\) which is at most \(\varepsilon\) in norm. Check out the Pseudospectra gateway and then do some pseudospectral experiments with Mandelbrot matrices.
# Pseudospectra of the simple eigenvalue problem, for problem 12
n = 7
M7 = m_mand(n)
nx, ny = (100, 100)
x = np.linspace(-2.5, 0.5, nx)
y = np.linspace(-1.25, 1.25, ny)
[X, Y] = np.meshgrid(x, y, indexing='ij')
Z = np.zeros((nx, ny))
for i in range(nx):
for j in range(ny):
_, temp, _ = scipy.linalg.svd(complex(X[i, j], Y[i, j])*np.eye(2**(n-1)-1) - M7)
Z[i, j] = temp[-1]
fig = plt.figure(figsize=(10, 8), dpi = 80)
plt.contour(X, Y, Z, np.logspace(-5, 0, 15))
plt.show()
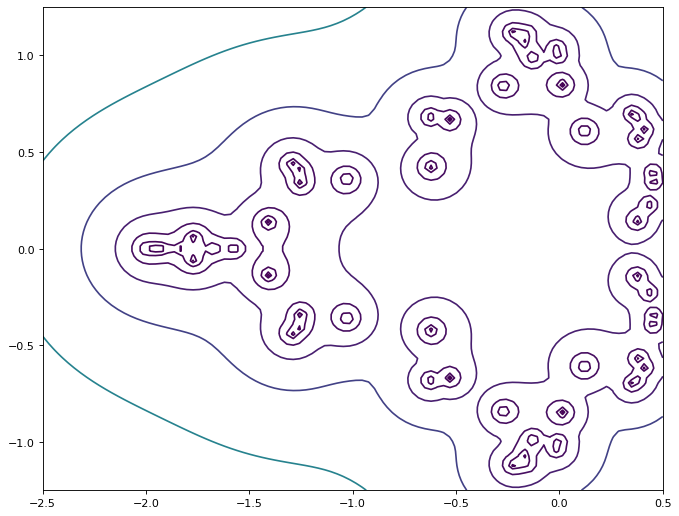
Mandelbrot Activity 13#
Other families of polynomials like the Mandelbrot polynomials can be defined: Fibonacci–Mandelbrot polynomials defined by \(q_{n+1}(z) = z q_n(z) q_{n-1}(z) + 1\) and \(q_0(z)=0\) and \(q_1(z) = 1\), for instance; or Fibonacci–Narayana polynomials. Define your own polynomials by recurrence relation, and find your own matrices whose eigenvalues are their roots, and draw their eigenvalues. We have only done a few of these, and there are infinitely many to choose from. It’s possible your results will be completely new (and therefore publishable).
Mandelbrot Activity 14#
The paper Some Facts and Conjectures on Mandelbrot Polynomials contains a formula for the Mandelbrot Generating Function MGF(k,c), which analytically solves the Mandelbrot iteration \(z_{n+1} = z_n^2 + c\), at least for \(c\) outside the Mandelbrot set. This means that we could (say) take half an iteration—and find \(z_{1/2}(c)\) or \(z_{3/2}(c)\). As with Stand-Up Math’s Video on Complex Fibonacci Numbers these are likely to be complex numbers. So far as we know, no-one (not even us) has computed these. Do so, for (say) \(c=1\) or \(c=2\). Plot the results. This, also, might be publishable (again, Maple Transactions might be a good place).
This could be very interesting. We lookforward to your solution!
Mandelbrot Activity 15#
A companion matrix for a polynomial (say \(P(\lambda)\)) is simply a matrix \(C\) whose eigenvalues are the roots of \(P(\lambda)\). Every matrix has a characteristic polynomial whose roots are its eigenvalues; what’s interesting is that this can be run the other way (it’s a bit more complicated because “Frobenius companion matrices” as in the link above have special properties). But companion matrices are not unique: any matrix similar to a companion matrix \(\mathbf{S}\mathbf{C}\mathbf{S}^{-1}\) is also a companion matrix for that same \(P(\lambda)\). Suppose that you have a polynomial with integer coefficients. Then the Frobenius companion matrix has (those same) integers as entries, together with ones and zeros. Therefore, out of all integer companion matrices for \(P(\lambda)\), there must be one with minimal height: the height of the matrix is the size of the largest absolute value of any entry in the matrix. Mandelbrot matrices as defined above have height \(1\), which is the smallest possible for integer companions, and are therefore “minimal height”. Note that the size of the coefficients of the polynomial are exponential in the degree! So the height of the Frobenius companion matrix of Mandelbrot polynomials is likewise exponential. Not much is known about minimal height companion matrices (see also our first paper); we do not have an algorithm for finding one for a given integer polynomial, for instance. We believe that minimal height companion matrices are generally better-conditioned as far as their eigenvalues, but we have no proof. Find a minimal height companion matrix for (say) \(\lambda^3 + 5\lambda^2 + 3\lambda + 1\). Find a general algorithm for computing minimal height companions. Prove that they’re useful. If you succeed at this problem, you should certainly publish your results; a good venue might be the Electronic Journal of Linear Algebra.
Similarly, we look forward to your solution!
Mandelbrot Activity 16#
Take some time and write down some of your own questions about this material.
What is the area of the Mandelbrot set? Does it even have an area? What is its perimeter? Does it even have a perimeter? What is its dimension? What is the fastest way to reliably compute the Mandelbrot set and draw a picture of it? Are there good free programs to do it? Is there a three-dimensional version of the Mandelbrot set? A four-dimensional version? What happens if you have a different power, say \(z^3+c\)? Or a fractional power, \(z^{1/2} + c\)? Is there a matrix version (it looks like the iteration \(Z^2 + \mathbf{C}\) makes sense for matrices \(\mathbf{C}\)). What is the most important open question about the Mandelbrot set? Who proved the most about the Mandelbrot set? About Mandelbrot polynomials? What’s the best way to solve Mandelbrot polynomials? Are there “Mandelbrot rational functions?” What element or elements of the Mandelbrot set has the largest imaginary part? What kind of number is it/are they (rational, irrational, algebraic, transcendental)?
