Welcome to Computational Discovery on Jupyter

Overture

In this section there are no definitions, no theorems, no computations. Well, not in this overture: just a picture, the an infinite number of infinity symbols below, and a little discussion of why we wrote this Open Educational Resource or book, and what you might get out of it.

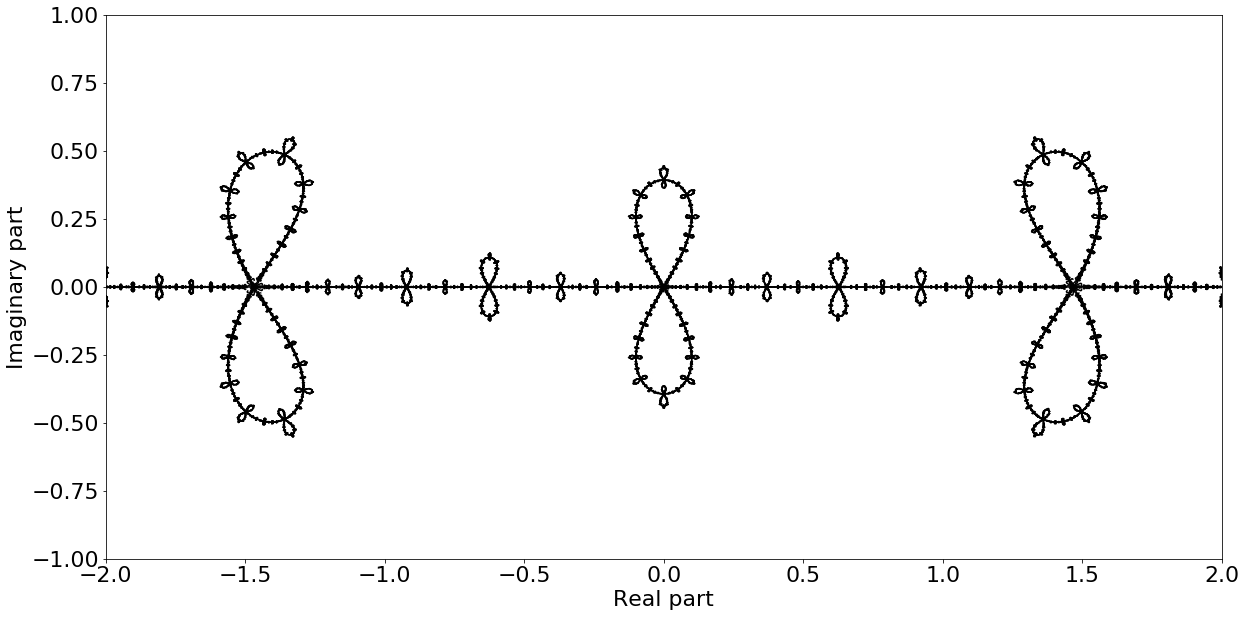
Fig. 1 Infinitely many infinity symbols

What’s in it for you?

We’ll be using Python to explore some interesting mathematics, mathematics not in the standard curriculum. So it’s an opportunity to learn a popular programming language. Why use mathematics, instead of some other science, like biology or physics or chemistry? Why not some engineering, or economics, or psychology, or music?

The truth of the matter is that math is the simplest out of all of those. You probably know that already. This is the fastest way to learn Python. You’ll wind up learning some other things too, but let’s start with that.

What’s in it for us?

Many of our students, when surveyed, say that they want to be taught “more programming” and for it to be taught earlier. This is an attempt to do so. Also, we feel that by offering some interesting mathematics straight away, which we can do owing to the powerful tools that we’re going to use, we might reach a larger audience for mathematics, and to keep people interested for longer. Math is useful for a lot of things, although we’re not going to focus on that part of it. Instead we’re going straight for the heart of mathematics.

What’s in it?

We’ll use videos, images, programs, programming activities, pencil-and-paper activities, and this Jupyter Book and the associated Jupyter Notebooks to present material for your inspection and interaction. We will encourage people to contribute their own notebooks to extend this material. Indeed some of the material that you will see was created/discovered/invented/published first by our students.

An Introductory Video